Get Calculus homework help – Post your homework assignment questions and get answers from qualified tutors

Introduction to Calculus
Calculus is a field in Mathematics that examines accumulation and change rates. It is an effective tool for comprehending how things evolve throughout time. Infinitesimal calculus is another name for calculus. Calculus homework help entiails the process of posting questions in the discipline online to get help from tutors. There are two primary areas of calculus;
- Differential Calculus
- Integral Calculus
Differential Calculus
This is an aspect of calculus that deals with rates and slopes of curves. It is the more complex one and most students find themselves asking or looking for Calculus homework help on this. It is based on how different quantities vary in connection to one another, especially when there is a dependency between two quantities.
As an example, if we have a function f (x) = 2x3 + 4x. In this case we need to find out the rate of change of the above function at a specific point, for instance when x = 3. Therefore, rate of change (slope) at x = 3, we use the derivative of the function, denoted as
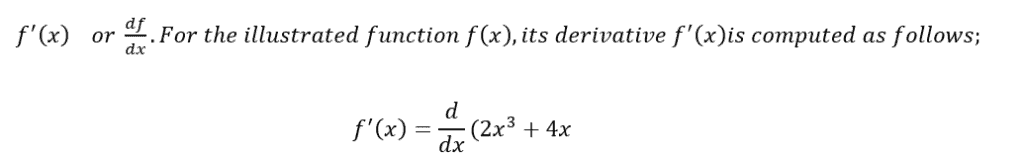
Use the power rule of differentiation to get:
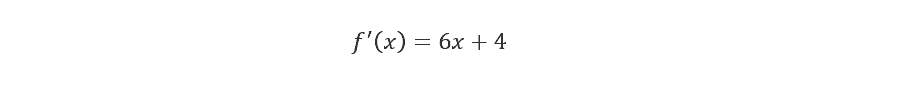
To find out the rate of change at x = 3, it is important to substitute x = 3 into the derivative:
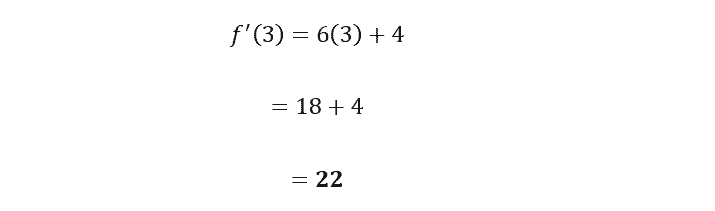
Therefore, at x = 3, the rate of change of the function f (x) = 2x3 + 4x is 22. In this illustration, differential calculus provides us with the slope of the tangent line to the curve at a given position, which helps us understand how the function f'(x) acts at that point.
There are various important topics covered under differential calculus and this includes the following:
Limits in calculus homework help
A limit is a key concept in differential calculus. It is employed to explain how a function behaves when its input gets closer to a particular value. From a mathematical perspective, the value that f (x) arbitrarily approaches as (x) arbitrarily approaches (c) is known as the limit of the function f (x) as x approaches (c). Therefore, a limit can be expressed using the limit formula as shown below;
limx→c f (x) = A
This is used to indicate that “the limit of f of x as x approaches c should be equivalent or equal to A”.
Derivatives
Derivatives essentially quantify the rate of change of a function with respect to one of its variables. In terms of geometry, it shows the tangent line’s slope to the function’s graph at a specific position. Mathematicians can examine motion, optimize functions, comprehend rates of change, and more with the help of derivatives. Also, the definition and comprehension of other crucial ideas like integration, optimization, and differential equations depend heavily on derivatives. There are various techniques that can be applied to calculate derivatives and this includes the following;
- Power rule – Used when a derivative is expressed in power form or raised to any power in this case. For example, d/dx = [ xn] = nXn-1
- Product rule – This is used when differentiating products of two or more functions. For example, d/dx (f(x). g(x)) = f’ (x). g(x) + f(x). g’ (x)
- Quotient rule – used when determining a derivative that has a fractional form. For example, d/dx [ 5x + 1/3x -4]
- Chain rule – Applied to a derivative with a function composition. For example, d/dx [(In x)n].
Continuity
A key idea in differential calculus that addresses a function’s smoothness is continuity. Formally, if a function f(x) is continuous at a point (c) then three of the following requirements must be satisfied;
- f(c) is defined at (c)
- The limit of f (x) as x approaches c exist
- The limit of f (x) as x approaches c is equivalent or equal to f (c)
Integral Calculus
Calculus’s idea of integration basically, determining the accumulation of quantities across a certain interval is the subject of integral calculus. When we are aware of the rate of change, we may use this inverse differentiation process to calculate the total amount of the object in question. The definite integral, or the area under a curve between two given points on the x-axis, is one of the basic ideas of integral calculus. It can be described as the limit of a sum of infinitely many small values and is represented by the integral symbol, ∫.
Illustration (1):
Let’s consider the function f (x) = x2. Find the area under the curve of this function between x = 0 and x = 2. In this case it advisable to use the definite integral:
∫02 x2 dx
By calculating this integral, the end result will be as shown below:
[x3/3]20 = 23/3 – 03/3 = 8/3
Therefore, the area under the curve of f’ (x) = x2 between x =0 and x = 2 as shown in the illustration above is 8/3. This is but one straightforward illustration of how areas, volumes, and other quantities that build during an interval can be found using integral calculus.
Application of Calculus
Solving optimization issues is a fundamental use of calculus. This entails determining a function’s maximum or minimum value, which is important in disciplines like physics and engineering. Calculus is used, for instance, in engineering to improve the design of equipment or structures in order to save costs and the same time increase efficiency. Let us look at a well-known illustration:
Maximizing a box’s size with a set quantity of material. Let’s say we are given a rectangular piece of cardboard that is (x by y) in size. We want to cut equal-sized squares out of each corner and fold the edges to make an open-top box. The resultant box’s size will be
S = x (2y – 2x).
Therefore, when we take the derivative of the area function with respect to x and set it equal to zero to locate critical points, from which we can calculate the sizes that maximize the volume of the open top box. Calculus optimization and differentiation techniques are both applied in this process.
Get assistance with Calculus homework help
There are quite a few websites that help with Calculus problems on the internet. However, majority of them do not offer detailed explanations and examples that are integral in this subject. It is thus paramount to look for a particular writing website that offers such. For any student looking to have exemplary Calculus homework help, yourhomeworksolutions has the best tutors in the field. These tutors offer direct explanations and provide numerous examples for any given Calculus question.



